





In the following, we give explicit examples of constellations for extremal, unpolarized, pure states for S = 1 to S = 10, corresponding to N = 2 to N = 20 photons. For all examples, the degree M of unpolarization, i.e., A(S)M = 0, is the highest we found, and it matches the largest degree t for which a spherical t design with N points is known to exist. For the parameters S listed in Table 1 of the article, we provide the details for the very same states. For the other cases, we list a state for which A(S)M = 0 and A(S)M+1 is non-zero, but minimal among the states found so far.
The state |Ψ(S)⟩ = ∑Sm = -S Ψm|S,m⟩ is given by the row vector with the 2S+1 coefficients [ Ψ-S,Ψ-S+1,…,ΨS ]. We also computed the cumulative squared lengths of the multipoles A(S)M. While we give exact algebraic expressions (with i = sqrt(-1)) for the state in most cases, we use floating point numbers for the constellation with N = 2S points. Finally, we provide information about the symmetry group of the constellation.
More examples can be found here.
Unfortuantely, there are some typos in the printed versions of the articles for S=2,5/2,3,5,9. Please let us know in case you noticed further typos.
|Ψ(1)⟩ = [ 0, 1, 0 ](unique solution, M = 1 is maximal)
A(1)M = [ 0, 2/3 ]
 constellation (radial line):
constellation (radial line):
[ 0.0, 0.0, 1.0 ] [ 0.0, 0.0, -1.0 ]
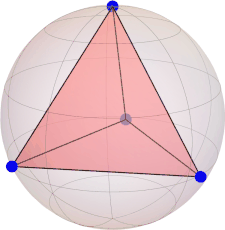
|Ψ(3/2)⟩ = [ sqrt(2)/2, 0, 0, sqrt(2)/2 ](unique solution, M = 1 is maximal)
A(3/2)M = [ 0, 1/4, 3/4 ]
 constellation (equatorial triangle):
constellation (equatorial triangle):
[ 0.5, -0.866025403784439, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.5, 0.866025403784439, 0.0 ]
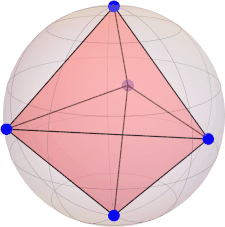
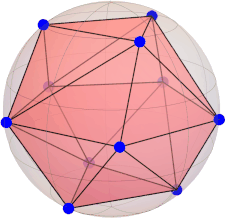
|Ψ(2)⟩ = [ 0, sqrt(6)/3, 0, 0, sqrt(3)/3 ](unique solution, M = 2 is maximal)
A(2)M = [ 0, 0, 1/2, 4/5 ]
 constellation (tetrahedron):
constellation (tetrahedron):
[ 0.0, 0.0, 1.0 ] [ 0.471404520791032, 0.816496580927726, -0.333333333333333 ] [ -0.942809041582063, 0.0, -0.333333333333333 ] [ 0.471404520791032, -0.816496580927726, -0.333333333333333 ]
|Ψ(5/2)⟩ = [ 0, sqrt(2)/2, 0, 0, sqrt(2)/2, 0 ](M = 1 is maximal)
AM(5/2) = [ 0, 1/84, 59/252, 5/9, 5/6 ]
≈ [ 0, 0.011905, 0.23413, 0.55556, 0.83334 ]
 constellation (equatorial triangle and poles):
constellation (equatorial triangle and poles):
[ 0.0, 0.0, 1.0 ] [ 0.5, -0.866025403784438, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.5, 0.866025403784438, 0.0 ] [ 0.0, 0.0, -1.0 ]
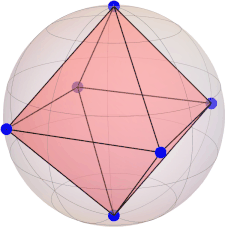
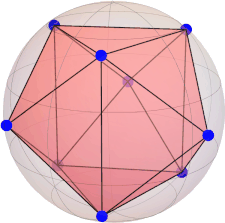
|Ψ(3)⟩ = [ 0, sqrt(2)/2, 0, 0, 0, -sqrt(2)/2, 0 ](unique solution, M = 3 is maximal)
A(3)M = [ 0, 0, 0, 6/11, 6/11, 5/7 ]
 constellation (octahedron):
constellation (octahedron):
[ 0.0, 0.0, 1.0 ] [ 1.0, 0.0, 0.0 ] [ 0.0, 1.0, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.0, -1.0, 0.0 ] [ 0.0, 0.0, -1.0 ]
|Ψ(7/2)⟩ = [ sqrt(2)/3, 0, 0, sqrt(14)/6, 0, 0, sqrt(14)/6, 0 ](M = 2 is maximal)
A(7/2)M = [ 0, 0, 49/264, 49/264, 49/143, 821/1144, 7/8 ]
≈ [ 0, 0, 0.18561, 0.18561, 0.34266, 0.71766, 0.875 ]
 constellation (two aligned triangles and pole):
constellation (two aligned triangles and pole):
[ 0.406731490944482, 0.704479607354083, 0.581616692587408 ] [ -0.813462981888963, 0.000000000000000, 0.581616692587408 ] [ 0.406731490944482, -0.704479607354083, 0.581616692587408 ] [ 0.485089093681821, 0.840198956454453, -0.242392831502497 ] [ -0.970178187363642, 0.000000000000000, -0.242392831502497 ] [ 0.485089093681821, -0.840198956454453, -0.242392831502497 ] [ 0.0, 0.0, -1.0 ]
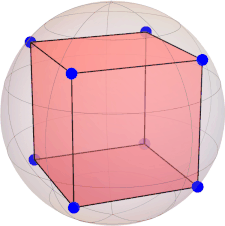
|Ψ(4)⟩ = [ sqrt(30)/12, 0, 0, 0, sqrt(21)/6, 0, 0, 0, sqrt(30)/12 ](M = 3 is maximal)
A(4)M = [ 0, 0, 0, 98/429, 98/429, 74/117, 74/117, 8/9 ]
≈ [ 0, 0, 0, 0.22844, 0.22844, 0.63248, 0.63248, 0.88889 ]
 constellation (cube):
constellation (cube):
[ 0.577350269189626, -0.577350269189626, 0.577350269189626 ] [ 0.577350269189626, 0.577350269189626, 0.577350269189626 ] [ -0.577350269189626, -0.577350269189626, 0.577350269189626 ] [ -0.577350269189626, 0.577350269189626, 0.577350269189626 ] [ 0.577350269189626, -0.577350269189626, -0.577350269189626 ] [ 0.577350269189626, 0.577350269189626, -0.577350269189626 ] [ -0.577350269189626, -0.577350269189626, -0.577350269189626 ] [ -0.577350269189626, 0.577350269189626, -0.577350269189626 ]
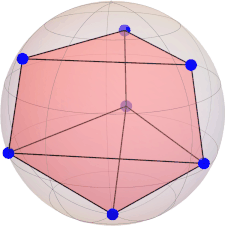
|Ψ(9/2)⟩ = [ sqrt(6)/6, 0, 0, -sqrt(3)/3, 0, 0, -sqrt(3)/3, 0, 0, sqrt(6)/6 ](M = 2 is maximal)
A(9/2)M ≈ [ 0, 0, 0.0064155, 0.028793, 0.35314, 0.45769, 0.45882, 0.73190, 0.9 ]
 constellation (three triangles):
constellation (three triangles):
[ -0.354635777076689, -0.614247184078495, 0.704935360489777 ] [ 0.709271554153378, 0.000000000000000, 0.704935360489777 ] [ -0.354635777076689, 0.614247184078495, 0.704935360489777 ] [ 0.5, 0.866025403784438, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.5, -0.866025403784438, 0.0 ] [ -0.354635777076689, -0.614247184078495, -0.704935360489777 ] [ 0.709271554153378, 0.000000000000000, -0.704935360489777 ] [ -0.354635777076689, 0.614247184078495, -0.704935360489777 ]
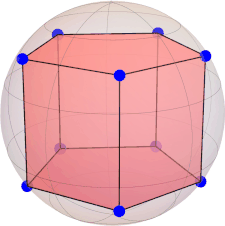
|Ψ(5)⟩ = [ sqrt(5)/5, 0, 0, 0, 0, sqrt(15)/5, 0, 0, 0, 0, sqrt(5)/5 ](M = 3 is maximal)
A(5)M ≈ [ 0, 0, 0, 0.12587, 0.18126, 0.21014, 0.53593, 0.60719, 0.70601, 0.90909 ]
 constellation (pentagonal prism):
constellation (pentagonal prism):
[ 0.659009385323091, 0.478798344791898, 0.580050665959984 ] [ -0.251719186288245, 0.774711995630481, 0.580050665959984 ] [ -0.814580398069693, 0.0, 0.580050665959984 ] [ -0.251719186288245, -0.774711995630481, 0.580050665959984 ] [ 0.659009385323091, -0.478798344791898, 0.580050665959984 ] [ 0.659009385323091, 0.478798344791898, -0.580050665959984 ] [ -0.251719186288245, -0.774711995630481, -0.580050665959984 ] [ -0.814580398069693, 0.0, -0.580050665959984 ] [ -0.251719186288245, 0.774711995630481, -0.580050665959984 ] [ 0.659009385323091, -0.478798344791898, -0.580050665959984 ]
|Ψ(11/2)⟩ = [ sqrt(17)/12, 0, 0, i sqrt(55)/12, 0, 0, 0, 0, i sqrt(55)/12, 0, 0, sqrt(17)/12 ](M = 3 is maximal)
A(11/2)M ≈ [ 0, 0, 0, 0.042193, 0.11612, 0.32001, 0.37254, 0.44398, 0.64454, 0.74368, 0.91666 ]
 constellation:
constellation:
[ -0.540468153848830, 0.312669120556627, 0.781109592647269 ] [ 0.001113638755064, -0.625130604696015, 0.780519369958951 ] [ 0.542329414861365, 0.312456964568204, 0.779903488304132 ] [ 0.808618504015847, 0.588101567578426, 0.016512455146701 ] [ -0.309745649254401, -0.950765489949400, 0.010129950110765 ] [ -1.0, 0.0, 0. ] [ -0.309745649254401, 0.950765489949400, -0.010129950110765 ] [ 0.808618504015847, -0.588101567578426, -0.016512455146701 ] [ 0.542329414861365, -0.312456964568204, -0.779903488304132 ] [ 0.001113638755064, 0.625130604696015, -0.780519369958951 ] [ -0.540468153848830, -0.312669120556627, -0.781109592647269 ]
|Ψ(6)⟩ = [ 0, sqrt(7)/5, 0, 0, 0, 0, sqrt(11)/5, 0, 0, 0, 0, -sqrt(7)/5, 0 ]
A(6)M = [ 0, 0, 0, 0, 0, 121/323, 121/323, 121/323, 121/323, 328/437, 328/437, 12/13 ]
≈ [ 0, 0, 0, 0, 0, 0.37461, 0.37461, 0.37461, 0.37461, 0.75057, 0.75057, 0.92308 ]
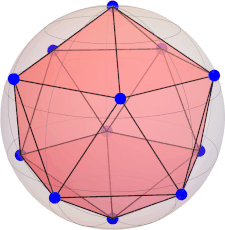
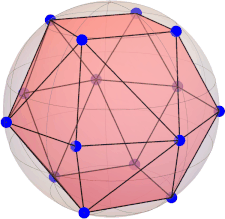
 constellation (dodecahedron):
constellation (dodecahedron):
[ 0.0, 0.0, 1.0 ] [ 0.723606797749979, 0.525731112119134, 0.447213595499958 ] [ -0.276393202250021, 0.850650808352040, 0.447213595499958 ] [ -0.894427190999916, 0.0, 0.447213595499958 ] [ -0.276393202250021, -0.850650808352040, 0.447213595499958 ] [ 0.723606797749979, -0.525731112119134, 0.447213595499958 ] [ -0.723606797749979, 0.525731112119134, -0.447213595499958 ] [ 0.276393202250021, 0.850650808352040, -0.447213595499958 ] [ 0.894427190999919, 0.0, -0.447213595499958 ] [ 0.276393202250021, -0.850650808352040, -0.447213595499958 ] [ -0.723606797749979, -0.525731112119134, -0.447213595499958 ] [ 0.0, 0.0, -1.0 ]
|Ψ(13/2)⟩ = [ sqrt(15)/15, 0, 0, i sqrt(390)/30, 0, 0, 0, 0, 0, 0, i sqrt(390)/30, 0, 0, sqrt(15)/15 ]
A(13/2)M = [ 0, 0, 0, 247/5610, 247/5610, 656123/3391500, 994123/3391500, 169/510, 16393/41055, 863083/1560090, 19999967/27858750, 459353/603750, 13/14 ]
≈ [ 0, 0, 0, 0.044028, 0.044028, 0.19346, 0.29312, 0.33137, 0.39929, 0.55322, 0.71790, 0.76083, 0.92857 ]
 constellation (bent heptagon and two twisted triangles above & below):
constellation (bent heptagon and two twisted triangles above & below):
[ -0.456786580721863, 0.263710287026873, 0.849589844683088 ] [ 0.456807478105276, 0.263753513416359, 0.849565190028184 ] [ 0.0, -0.527463766250099, 0.849577527106852 ] [ 0.900976971397839, 0.433818742643517, 0.006464947174969 ] [ 0.222653721362577, -0.974883834307386, 0.005179765392943 ] [ -0.623400079035304, 0.781897753601443, 0.002871301411168 ] [ -1.0, 0.0, 0.0 ] [ -0.623400079035304, -0.781897753601443, -0.002871301411168 ] [ 0.222653721362577, 0.974883834307386, -0.005179765392943 ] [ 0.900976971397839, -0.433818742643517, -0.006464947174970 ] [ 0.0, 0.527463766250099, -0.849577527106852 ] [ 0.456807478105276, -0.263753513416359, -0.849565190028184 ] [ -0.456786580721863, -0.263710287026873, -0.849589844683088 ]
|Ψ(7)⟩ = [ 0.0, 0.484038792672727, 0.0, 0.0, -0.217868005816070 + 0.228902507261237 i, 0.0, 0.0, 0.277562504208005 + 0.504624909270376 i, 0.0, 0.0, -0.217868005816070 + 0.228902507261237 i, 0.0, 0.0, 0.484038792672727, 0.0 ]
A(7)M ≈ [ 0, 0, 0, 0, 0.022088, 0.16322, 0.24969, 0.33424, 0.38239, 0.44336, 0.54533, 0.71629, 0.79733, 0.93333 ]
 constellation (four triangles and the two poles):
constellation (four triangles and the two poles):
[ 0.0, 0.0, 1.0 ] [ 0.768016179259059, 0.239363858169746, 0.594016912047470 ] [ -0.591303271552385, 0.545439592670935, 0.594016912047470 ] [ -0.176712907706674, -0.784803450840680, 0.594016912047470 ] [ 0.117497703154367, 0.945457109922784, 0.303817614778843 ] [ 0.760041023804564, -0.574484550779396, 0.303817614778843 ] [ -0.877538726958931, -0.370972559143387, 0.303817614778843 ] [ 0.117497703154367, -0.945457109922784, -0.303817614778843 ] [ 0.760041023804564, 0.574484550779396, -0.303817614778843 ] [ -0.877538726958931, 0.370972559143387, -0.303817614778843 ] [ -0.591303271552385, -0.545439592670935, -0.594016912047470 ] [ -0.176712907706674, 0.784803450840680, -0.594016912047470 ] [ 0.768016179259059, -0.239363858169746, -0.594016912047470 ] [ 0.0, 0.0, -1.0 ]
|Ψ(15/2)⟩ = [ 3/44 sqrt(22), 0, 0, 0, sqrt(770)/44, 0, 0, 0, 0, 0, 0, sqrt(770)/44, 0, 0, 0, 3/44 sqrt(22)]
A(15/2)M ≈ [ 0, 0, 0, 0.0039210, 0.0039210, 0.13265, 0.20292, 0.29853, 0.34431, 0.39883, 0.46949, 0.57603, 0.75148, 0.79966, 0.93750 ]
 constellation (heptagon and two aligned square above & below):
constellation (heptagon and two aligned square above & below):
[ 0.433217774817543, 0.433301918821350, 0.790298555438306 ] [ 0.433217774817543, -0.433301918821350, 0.790298555438306 ] [ -0.433368690130957, -0.433284237986233, 0.790225504224502 ] [ -0.433368690130957, 0.433284237986233, 0.790225504224502 ] [ 0.219585359474376, 0.975593291235907, 0.0 ] [ -0.622122481482076, 0.782919930794065, 0.0 ] [ 0.902631297489889, 0.430414614983877, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.902631297489889, -0.430414614983877, 0.0 ] [ -0.622122481482076, -0.782919930794065, 0.0 ] [ 0.219585359474376, -0.975593291235907, 0.0 ] [ 0.433217774817543, 0.433301918821350, -0.790298555438306 ] [ 0.433217774817543, -0.433301918821350, -0.790298555438306 ] [ -0.433368690130957, -0.433284237986233, -0.790225504224502 ] [ -0.433368690130957, 0.433284237986233, -0.790225504224502 ]
|Ψ(8)⟩ = [ sqrt(69)/32, 0, -7/1472 i sqrt(3358)+17/1472 sqrt(690), 0, 3/4784 i sqrt(152789)-1/1196 sqrt(31395), 0, -1/210496 i sqrt(50420370)-279/210496 sqrt(46046), 0, 7/26312 i sqrt(480194)-137/105248 sqrt(98670), 0, 1/210496 i sqrt(50420370)+279/210496 sqrt(46046), 0, 3/4784 i sqrt(152789)-1/1196 sqrt(31395), 0, 7/1472 i sqrt(3358)-17/1472 sqrt(690), 0, sqrt(69)/32 ]
A(8)M ≈ [ 0, 0, 0, 0, 0, 0.066374, 0.21902, 0.24823, 0.31960, 0.36874, 0.37228, 0.51437, 0.66655, 0.70602, 0.82630, 0.94118 ]
 constellation:
constellation:
[ -0.146859793851903, 0.403430399755151, 0.903147891268742 ] [ 0.146859793851903, -0.403430399755151, 0.903147891268742 ] [ 0.816496580927726, 0.0, 0.577350269189626 ] [ -0.816496580927726, 0.0, 0.577350269189626 ] [ 0.510336695378834, 0.766907301282083, 0.389113927520006 ] [ -0.510336695378834, -0.766907301282083, 0.389113927520006 ] [ -0.363476901526931, 0.913767095133985, 0.181422815287328 ] [ 0.363476901526931, -0.913767095133985, 0.181422815287328 ] [ -0.913767095133985, 0.363476901526931, -0.181422815287328 ] [ 0.913767095133985, -0.363476901526931, -0.181422815287328 ] [ 0.766907301282083, 0.510336695378834, -0.389113927520006 ] [ -0.766907301282083, -0.510336695378834, -0.389113927520006 ] [ 0.0, 0.816496580927726, -0.577350269189626 ] [ 0.0, -0.816496580927726, -0.577350269189626 ] [ -0.403430399755151, 0.146859793851903, -0.903147891268742 ] [ 0.403430399755151, -0.146859793851903, -0.903147891268742 ]
|Ψ(17/2)⟩ = [ 0.0, 0.435874159108882, 0.0, 0.0, -0.158009774587788 + 0.300431770262860 i, 0.0, 0.0, 0.438536379196716 - 0.0497315201215425 i, 0.0, 0.0, 0.438536379196716 - 0.0497315201215425 i, 0.0, 0.0, -0.158009774587788 + 0.300431770262860 i, 0.0, 0.0, 0.435874159108882, 0.0 ]
A(17/2)M ≈ [ 0, 0, 0, 0, 0.024845, 0.090384, 0.11317, 0.20352, 0.26268, 0.32590, 0.40828, 0.48103, 0.52997, 0.60888, 0.75945, 0.83311, 0.94444 ]
 constellation (five triangles plus the two poles):
constellation (five triangles plus the two poles):
[ 0.0, 0.0, 1.0 ] [ -0.602115369310431, 0.430511934776098, 0.672396130309734 ] [ 0.673891956803705, 0.306191238443833, 0.672396130309734 ] [ -0.071776587493275, -0.736703173219931, 0.672396130309734 ] [ -0.162582048449742, 0.902577354866469, 0.398649214227414 ] [ 0.862945942419795, -0.310488493276445, 0.398649214227414 ] [ -0.700363893970053, -0.592088861590024, 0.398649214227414 ] [ 0.5, 0.866025403784438, 0.0 ] [ -1.0, 0.0, 0.0 ] [ 0.5, -0.866025403784438, 0.0 ] [ -0.700363893970053, 0.592088861590024, -0.398649214227414 ] [ 0.862945942419795, 0.310488493276445, -0.398649214227414 ] [ -0.162582048449742, -0.902577354866469, -0.398649214227414 ] [ -0.071776587493275, 0.736703173219931, -0.672396130309734 ] [ 0.673891956803705, -0.306191238443833, -0.672396130309734 ] [ -0.602115369310431, -0.430511934776098, -0.672396130309734 ] [ 0.0, 0.0, -1.0 ]
|Ψ(9)⟩ = [ sqrt(455)/65, 0, 0, 0, 0, i sqrt(6630)/130, 0, 0, 0, 0, 0, 0, 0, i sqrt(6630)/130, 0, 0, 0, 0, sqrt(455)/65 ]
A(9)M ≈ [ 0, 0, 0, 0, 0, 0.081787, 0.081787, 0.21370, 0.21370, 0.32413, 0.32413, 0.45360, 0.45360, 0.58772, 0.58772, 0.82262, 0.82262, 0.94736 ]
 constellation (slightly bent equatorial octagon and two flat pentagons above & below):
constellation (slightly bent equatorial octagon and two flat pentagons above & below):
[ -0.600064784923290, -0.194953054131990, 0.775832172946943 ] [ 0.0, -0.630894385012959, 0.775868722761216 ] [ 0.600064784923290, -0.194953054131990, 0.775832172946943 ] [ 0.370865130063146, 0.510400251630871, 0.775854779219919 ] [ -0.370865130063146, 0.510400251630871, 0.775854779219919 ] [ -0.923876304082174, -0.382688993090229, 0.001307410818663 ] [ -0.382677490170340, -0.923881835161757, -0.000541456436505 ] [ 0.382677490170340, -0.923881835161757, -0.000541456436505 ] [ 0.923876304082174, -0.382688993090229, 0.001307410818663 ] [ 0.923876304082174, 0.382688993090229, -0.001307410818663 ] [ 0.382677490170340, 0.923881835161757, 0.000541456436505 ] [ -0.382677490170340, 0.923881835161757, 0.000541456436505 ] [ -0.923876304082174, 0.382688993090229, -0.001307410818663 ] [ -0.600064784923290, 0.194953054131990, -0.775832172946943 ] [ 0.0, 0.630894385012959, -0.775868722761216 ] [ 0.600064784923290, 0.194953054131990, -0.775832172946943 ] [ 0.370865130063146, -0.510400251630871, -0.775854779219919 ] [ -0.370865130063146, -0.510400251630871, -0.775854779219919 ]
|Ψ(19/2)⟩ = [ 0.0, 0.394790292433844, 0.0, 0.0, 0.0, 0.533445903570947 + 0.0699184736916915 i, 0.0, 0.0, 0.0, -0.0634904625134868 + 0.0797470135479915 i, 0.0, 0.0, 0.0, 0.650420537037385, 0.0, 0.0, 0.0, 0.0, 0.0, 0.348209706929603 ]
A(19/2)M ≈ [ 0, 0, 0, 0, 0.024892, 0.059595, 0.073605, 0.17021, 0.19811, 0.25225, 0.30899, 0.37421, 0.45820, 0.53688, 0.57819, 0.63019, 0.78372, 0.85237, 0.95000 ]
 constellation (bent equatorial octagon, hexagon below, square above, and pole):
constellation (bent equatorial octagon, hexagon below, square above, and pole):
[ 0.0, 0.0, 1.0 ] [ -0.485306671181903, 0.514193954201776, 0.707164770310770 ] [ 0.514193950997086, 0.485306679117874, 0.707164767194738 ] [ 0.485306671181903, -0.514193954201776, 0.707164770310770 ] [ -0.514193950997086, -0.485306679117874, 0.707164767194738 ] [ -0.363347596778625, 0.924375137638232, 0.116228777983327 ] [ 0.924499195547427, 0.363089900543646, 0.116047238465058 ] [ 0.363347596778625, -0.924375137638232, 0.116228777983327 ] [ -0.924499195547427, -0.363089900543646, 0.116047238465058 ] [ -0.338774094909787, -0.940223561578101, 0.034810441988656 ] [ -0.940469942586444, 0.338121781084990, 0.034495626496208 ] [ 0.338774094909787, 0.940223561578101, 0.034810441988656 ] [ 0.940469942586444, -0.338121781084990, 0.034495626496208 ] [ 0.000563459578012, -0.670741144911577, -0.741691309802137 ] [ 0.580440369683931, -0.335915107176755, -0.741788391666796 ] [ 0.580115578771631, 0.335075664091756, -0.742421857571505 ] [ -0.000563459578012, 0.670741144911577, -0.741691309802137 ] [ -0.580440369683931, 0.335915107176755, -0.741788391666796 ] [ -0.580115578771631, -0.335075664091756, -0.742421857571505 ]
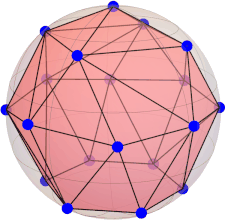
|Ψ(10)⟩ = [ sqrt(561)/75, 0, 0, 0, 0, sqrt(209)/25, 0, 0, 0, 0, sqrt(741)/75, 0, 0, 0, 0, -sqrt(209)/25, 0, 0, 0, 0, sqrt(561)/75 ]
A(10)M ≈ [ 0, 0, 0, 0, 0, 0.093330, 0.093330, 0.093330, 0.093330, 0.27876, 0.27876, 0.43038, 0.43038, 0.43038, 0.43038, 0.65514, 0.65514, 0.83394, 0.83394, 0.95238 ]
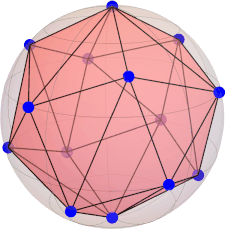
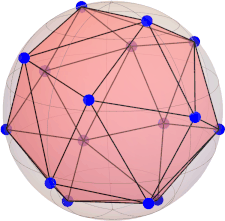
 constellation (dodecahedron):
constellation (dodecahedron):
[ 0.491123473188423, 0.356822089773090, 0.794654472291766 ] [ -0.187592474085080, 0.577350269189626, 0.794654472291766 ] [ -0.607061998206686, 0.0, 0.794654472291766 ] [ -0.187592474085080, -0.577350269189626, 0.794654472291766 ] [ 0.491123473188423, -0.356822089773090, 0.794654472291766 ] [ 0.794654472291766, 0.577350269189626, 0.187592474085080 ] [ -0.303530999103343, 0.934172358962716, 0.187592474085080 ] [ -0.982246946376846, 0.0, 0.187592474085080 ] [ -0.303530999103343, -0.934172358962716, 0.187592474085080 ] [ 0.794654472291766, -0.577350269189626, 0.187592474085080 ] [ -0.794654472291766, 0.577350269189626, -0.187592474085080 ] [ 0.303530999103343, 0.934172358962716, -0.187592474085080 ] [ 0.982246946376846, 0.0, -0.187592474085080 ] [ 0.303530999103343, -0.934172358962716, -0.187592474085080 ] [ -0.794654472291766, -0.577350269189626, -0.187592474085080 ] [ -0.491123473188423, 0.356822089773090, -0.794654472291766 ] [ 0.187592474085080, 0.577350269189626, -0.794654472291766 ] [ 0.607061998206686, 0.0, -0.794654472291766 ] [ 0.187592474085080, -0.577350269189626, -0.794654472291766 ] [ -0.491123473188423, -0.356822089773090, -0.794654472291766 ]